7.4. Representational Similarity Analysis#
Version 1.0
December 2024
License: GNU General Public License v3
This notebook is designed to be a beginner-friendly introduction to representational similarity analysis (RSA) that does not assume any prior knowledge of or familiarity with RSA. In this notebook, I walk you through the entire process of performing a basic representational similarity analysis. In particular, you will learn …
how to collect intermediate activations from neural networks (e.g., ResNet-50, ViT-B/16) using PyTorch,
how to compute representational dissimilarity matrices (RDMs) from these activations, and
how to compare multiple RDMs to each other.
Along the way, you will also learn to visualize the results of your analysis. Additional exercises are provided at the end of this notebook to help you become more comfortable with RSA.
By the end of this notebook, you should be able to interpret the main results of studies that use RSA as part of their analyses, and you should feel comfortable performing a basic analysis yourself. If you want to learn more about RSA after finishing this notebook, I have compiled a list of research articles at the very end of this notebook that you can explore to get started.
Why RSA?#
Understanding how the brain encodes and processes information is one of the central challenges in cognitive neuroscience. A growing body of research suggests that the brain does not represent information in discrete, isolated regions, but rather through distributed patterns of neural activity (Haxby et al., 2000; Mesulam, 1990; Sporns et al., 2005). This view has led to the development of multivariate analysis techniques that can assess the complex relationships between patterns of neural activation. One such technique is Representational Similarity Analysis (RSA), which studies the structure of neural representations by comparing the similarity of activity patterns across different experimental conditions or stimuli (Kriegeskorte et al., 2008).
RSA was introduced by Kriegeskorte et al. (2008) as a way to compare representational geometries (how neural activation patterns for different stimuli relate to each other) in high-dimensional brain data, such as functional MRI (fMRI). Rather than focusing on the activity of individual voxels, RSA examines the pattern of activity across brain areas (i.e., multiple voxels) to reveal how the brain organizes information. Specifically, RSA is a two-step process that involves (1) calculating the dissimilarity between activation patterns across conditions or stimuli, and (2) comparing these dissimilarities to those predicted by computational models, stimulus properties, or behavior (Kriegeskorte et al., 2008; Nili et al., 2014).

The major methodological advantage of RSA is its ability to abstract away the spatial dimension of the data to which it is applied (e.g., fMRI data, computational model outputs). In doing so, it avoids what is known in systems neuroscience as the spatial correspondence problem: Which unit in the measured brain data (e.g., individual voxels) corresponds to which unit in the computational model that is being studied? Note that RSA does not solve this problem, it just avoids it. The authors themselves refer to this as the “representational dissimilarity trick” in a later review of their technique (Kriegeskorte & Kievit, 2013). Technically speaking, RSA studies second-order isomorphisms (Shepard and Chipman, 1970) instead of first-order isomorphisms. While first-order isomorphisms capture the relationship between stimuli and their representations (How is a given stimulus represented?), second-order isomorphisms attempt to establish a relationship between these first-order isomorphisms (Are two stimuli represented similarly?).
The flexibility and broad applicability of RSA has led to its widespread adoption in cognitive neuroscience. RSA is increasingly being used to study various aspects of neural coding, including how the brain represents abstract concepts, processes dynamic sensory input, and organizes categorical information. If you’re curious about how RSA works but have no prior knowledge of it, this notebook is for you!
Prerequisites & Preparations#
Imports#
The following packages (listed in alphabetical order) need to be installed to run this notebook:
Matplotlib is a comprehensive library for creating static, animated, and interactive visualizations.
NumPy is a package for scientific computing with Python.
PyTorch is an open source machine learning framework.
SciPy provides fundamental algorithms for scientific computing in Python.
scikit-learn is a Python module for machine learning built on top of SciPy.
Seaborn is a Python data visualization library based on matplotlib that provides a high-level interface for drawing attractive and informative statistical graphics.
Torchvision consists of popular datasets, model architectures, and common image transformations for computer vision.
Let’s import these packages first. When doing so, we follow the standard practice of grouping imports in the following order:
standard library imports
related third party imports
local application/library specific imports (not applicable here)
import random
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import torch
import torchvision
from matplotlib.colors import Normalize
from scipy.stats import percentileofscore, spearmanr
from sklearn.manifold import MDS
from torchvision.models.feature_extraction import create_feature_extractor
from torchvision.transforms import v2
Compute Device#
device = torch.device(
'cuda' if torch.cuda.is_available() else
'mps' if torch.backends.mps.is_available() else
'cpu'
)
Downloading Networks#
Before we get started, we download all the pre-trained networks that we’ll use in this tutorial. These are:
AlexNet from One weird trick for parallelizing convolutional neural networks, originally proposed in ImageNet Classification with Deep Convolutional Neural Networks
ResNet-50 from Deep Residual Learning for Image Recognition
VGG11 from Very Deep Convolutional Networks for Large-Scale Image Recognition
ViT-B/16 from An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
# AlexNet
alexnet_weights = torchvision.models.AlexNet_Weights.IMAGENET1K_V1
alexnet = torchvision.models.alexnet(weights=alexnet_weights).eval().to(device)
alexnet_trafo = alexnet_weights.transforms()
# ResNet-50
resnet50_weights = torchvision.models.ResNet50_Weights.IMAGENET1K_V2
resnet50 = torchvision.models.resnet50(weights=resnet50_weights).eval().to(device)
resnet50_trafo = resnet50_weights.transforms()
# VGG11
vgg11_weights = torchvision.models.VGG11_Weights.IMAGENET1K_V1
vgg11 = torchvision.models.vgg11(weights=vgg11_weights).eval().to(device)
vgg11_trafo = vgg11_weights.transforms()
# ViT-B/16
vit_b16_weights = torchvision.models.ViT_B_16_Weights.IMAGENET1K_V1
vit_b16 = torchvision.models.vit_b_16(weights=vit_b16_weights).eval().to(device)
vit_b16_trafo = vit_b16_weights.transforms()
The following block of code is only relevant for Mac users and is necessary due to the fact that, at the time of writing this tutorial, the aten::_upsample_bilinear2d_aa.out operator (which is part of all transforms in the code block above) was not implemented for MPS. To make matters worse, the recommended temporary fix of setting the environment variable PYTORCH_ENABLE_MPS_FALLBACK=1 to use the CPU as a fallback did not work either. Hence, when using MPS, we move all tensors to the CPU first, then apply the transforms, and then move the tensors back to the GPU. That way, we can at least take advantage of MPS when performing the forward passes through the networks.
if device.type == 'mps':
# Define transforms to move tensors across devices
to_cpu = v2.Lambda(lambda x: x.to('cpu'))
to_mps = v2.Lambda(lambda x: x.to('mps'))
# Modify preset transforms
alexnet_trafo = v2.Compose([to_cpu, alexnet_trafo, to_mps])
resnet50_trafo = v2.Compose([to_cpu, resnet50_trafo, to_mps])
vgg11_trafo = v2.Compose([to_cpu, vgg11_trafo, to_mps])
vit_b16_trafo = v2.Compose([to_cpu, vit_b16_trafo, to_mps])
CIFAR10#
For this introductory tutorial, we will use images from the CIFAR10 dataset. To get started, we download the dataset from torchvision.
# Equivalent to ToTensor() in v1 of torchvision.transforms
to_tensor = v2.Compose([
v2.ToImage(),
v2.ToDtype(torch.float32, scale=True)
])
# Download CIFAR10 test set (1,000 images per class)
cifar10 = torchvision.datasets.CIFAR10(
root='./data',
train=False,
download=True,
transform=to_tensor
)
Files already downloaded and verified
We won’t be using the CIFAR10 dataset in its entirety. Instead, we only select a few images per class to use in the RSA analysis.
# Choose number of images to use from each class
num_images_per_class = 10
# Create dictionary to store selected images
num_classes = len(cifar10.classes)
images_by_class = {idx: [] for idx in range(num_classes)}
# Shuffle CIFAR10 dataset
random.seed(42)
indices = list(range(len(cifar10)))
random.shuffle(indices)
# Select first 10 images (after shuffling) of each class
subset_indices = []
for idx in indices:
img, label = cifar10[idx]
if len(images_by_class[label]) < 10:
images_by_class[label].append((img, label))
subset_indices.append(idx)
# Flatten images and labels into single tensors each
images, labels = zip(*[item for sublist in images_by_class.values() for item in sublist])
images = torch.stack(images)
labels = torch.tensor(labels)
Let us take a look at the images that we’ll be using from here on out.
fig, axes = plt.subplots(num_classes, num_images_per_class, figsize=(num_images_per_class / 2, num_classes / 2))
for row in range(num_classes):
for col in range(num_images_per_class):
img = images[row * num_images_per_class + col]
ax = axes[row, col]
ax.imshow(img.permute(1, 2, 0))
ax.axis('off')
plt.subplots_adjust(wspace=0.1, hspace=0.1)
plt.show()

Finally, let’s store the selected images along with their labels in a dictionary for later use.
cifar10_mini = {
'images': images.to(device),
'labels': labels.to(device)
}
Case Study: Comparing Network Representations#
To illustrate how RSA can be used to compare representational geometries, we focus on the simple setup of comparing multiple deep neural networks to each other. That way, we avoid the additional work that is required when dealing with fMRI data (preprocessing, averaging across participants, etc.). In particular, we will compare the representations learned by the penultimate layers of four different network architectures: AlexNet, ResNet-50, VGG11, and ViT-B/16. Note that the first three are all convolutional neural networks (CNNs), whereas ViT-B/16 is based on the transformer architecture. Do all three CNNs share similar representations? If so, is it different to the one learned by ViT-B/16? Let’s find out!
Outline#
As mentioned in the introduction of this notebook, RSA is a two-step process. In the first step, we compare the activation patterns elicited by two systems in response to the same set of stimuli within each system. Precisely, for each system (e.g., brain, computational model) we compare the activity pattern elicited by the \(i\)-th stimulus to the activity pattern of the \(j\)-th stimulus for all distinct pairs of stimuli \(i \neq j\). These pairwise dissimilarities are then arranged in a square matrix, called the representational dissimilarity matrix, which is indexed by the stimuli that were used to probe the system. In the second step, these matrices (one for each system) are then quantitatively compared to each other. This process is visualized in the figure below.

Step 0: Collecting Data#
Every RSA analysis will require data collection. Depending on the systems that are to be compared, this can be more or less expensive and time-consuming. If one is interested in analyzing DNNs, data collection amounts to a simple forward pass through the network, which is computationally cheap (assuming that pre-trained networks are used) and requires little time. Similarly, if one wants to analyze brain data (e.g., fMRI, EEG), there are several datasets available online that are ready-to-use (e.g., Natural Scenes Dataset, THINGS datasets). On the contrary, if one wants to analyze a new DNN architecture that needs to be trained from scratch or one wants to record new brain data, data collection can quickly become time-consuming and expensive.

In this tutorial, we will restrict ourselves to comparing the representations learned by different DNNs that have all been trained on the ImageNet dataset. To extract intermediate activations, we use the create_feature_extractor function. We start by extracting intermediate activations of AlexNet.
Note: AlexNet outputs a tensor of length 1,000 as it was trained on ImageNet (which has 1,000 classes). If we wanted to perform classification on the CIFAR10 dataset, we would have to replace the final linear layer with one that outputs a vector of length 10, and then fine-tune this layer on CIFAR10. However, we are solely interested in the internal representations (features) that AlexNet has learned from being trained on ImageNet, and we probe this learned representation by using images from the CIFAR10 dataset. Hence, we can use AlexNet as is, without any modifications to its architecture or weights. The same applies to the remaining architectures.
# Create feature extractor
feature_extractor = create_feature_extractor(
model=alexnet,
return_nodes={'classifier.5': 'penultimate_layer'}
)
# Perform forward pass with appropriate transform
# NOTE: We detach the output from the computational graph, as we won't need any gradients later on.
alexnet_activations = feature_extractor(
alexnet_trafo(cifar10_mini['images'])
)['penultimate_layer'].detach()
Let’s inspect the activations that we have extracted to make sure that everything works as expected. The penultimate layer of AlexNet outputs a vector of length 4,096. Since we passed a batch of 100 images to the network, we expect to extract a tensor of shape \(100 \times 4096\). Indeed, this is what we end up with:
display(alexnet_activations.shape)
torch.Size([100, 4096])
Let’s repeat this step for the remaining networks. We store all activations in a single dictionary, as this makes it easier to work with the data later on.
# Set up dictionary to store all activations
activations = {
'alexnet': alexnet_activations
}
# Set up variables to loop over
models = [resnet50, vgg11, vit_b16]
return_nodes = [
{'avgpool': 'penultimate_layer'}, # ResNet
{'classifier.4': 'penultimate_layer'}, # VGG
{'encoder.ln': 'penultimate_layer'} # ViT
]
trafos = [resnet50_trafo, vgg11_trafo, vit_b16_trafo]
names = ['resnet50', 'vgg11', 'vit_b16']
# Loop over all models
for m, r, t, n in zip(models, return_nodes, trafos, names):
# Create feature extractor
feature_extractor = create_feature_extractor(
model=m,
return_nodes=r
)
# Perform forward pass and store activations
activations[n] = feature_extractor(
t(cifar10_mini['images'])
)['penultimate_layer'].detach() # no need for gradients here
Again, let’s make sure that all activation tensors are as expected.
for k, v in activations.items():
print(f'{k}: {v.shape}')
alexnet: torch.Size([100, 4096])
resnet50: torch.Size([100, 2048, 1, 1])
vgg11: torch.Size([100, 4096])
vit_b16: torch.Size([100, 197, 768])
Note two things here.
First, the activation tensor produced by ResNet-50 carries two additional singleton dimensions (i.e., dimensions of size 1). This results from the fact that we extract the activations produced by an AdaptiveAvgPool2d layer with output size \((1, 1)\). Effectively, this layer takes as input a tensor of shape \((B, C, H, W)\), where \(B\) is the batch size, \(C\) is the number of channels, and \(H\) and \(W\) are the spatial dimensions, and then averages across the entire spatial resolution for each image and each channel. In our example, this reduces a tensor of shape \((100, 2048, 7, 7)\) to a tensor of shape \((100, 2048, 1, 1)\). To remove the redundant dimensions, we simply apply the squeeze function available in PyTorch.
Second, the activation tensor produced by ViT-B/16 has a different structure compared to the three CNNs altogether. This is because the Vision Transformer (ViT) architecture processes images as sequences of individual patches rather than as a single grid of pixels. More precisely, ViT divides an input image into a sequence of fixed-size patches, which are then linearly embedded into vectors. These vectors are concatenated with a special classification token (CLS token) and positional embeddings (these essentially let ViT know which image patch belongs where in the original image), forming the input sequence to the transformer encoder. The output of the transformer encoder is a sequence of vectors, where the first vector corresponds to the CLS token. Hence, we end up with a tensor of shape \((B, N, D)\), where \(B\) is the batch size, \(N\) is one more than the number of patches (due to the additional CLS token), and \(D\) is the embedding dimension. In our case, we have \(B = 100\) images and \(N = 197\) vectors of length \(D = 768\). The ViT-B/16 architecture uses patches of size \(16 \times 16\). Since we need \((224 / 16)^2 = 196\) of these to cover the entire image, we end up with \(N = 196 + 1\) vectors. The CLS token is used for classification tasks and represents the entire image. For that reason, we extract the activations corresponding to the CLS token for further analysis.
activations['resnet50'] = torch.squeeze(activations['resnet50']) # remove singleton dimensions
activations['vit_b16'] = activations['vit_b16'][:, 0, :] # extract CLS token
# Let's check again
for k, v in activations.items():
print(f'{k}: {v.shape}')
alexnet: torch.Size([100, 4096])
resnet50: torch.Size([100, 2048])
vgg11: torch.Size([100, 4096])
vit_b16: torch.Size([100, 768])
That’s it! We have all the data we need to perform our representational similarity analysis! Next, we need to compute the pairwise dissimilarities of the activations produced by each network, to capture each network’s representational geometry.
Step 1: Computing Pairwise Dissimilarities#
To capture the representational geometries of the networks we have probed (more precisely, of their penultimate layers), we need to compute the representational dissimilarity matrix (RDM) produced by each network. The RDM is a square \(N \times N\) matrix, where \(N\) is the number of stimuli that was used to probe the network (or, more general, the system we’re interested in). The entry at position \((i, j)\) for \(i, j \in \{1, \dots, N\}\) is the dissimilarity \(d(\mathbf{x}_i, \mathbf{x}_j)\) between the activity patterns produced by the \(i\)-th and \(j\)-th stimulus. This dissimilarity is quantified using a distance function \(d\). This function does not necessarily have to be a distance function in the mathematical sense (see here), but it is usually assumed to be symmetric, meaning that it outputs the same value irrespective of the order of the arguments being passed to it, i.e., \(d(\mathbf{x}_i, \mathbf{x}_j) = d(\mathbf{x}_j, \mathbf{x}_i)\). Additionally assuming that the distance from a point \(\mathbf{x}\) to itself is always zero (i.e., \(d(\mathbf{x}, \mathbf{x}) = 0\)), an RDM is a symmetric matrix with \(0\)s on the diagonal as depicted below.

For this tutorial, we will use Euclidean distance to compute the RDMs. Be aware that there exist many more distances that are commonly used in practice, and that the choice of the appropriate metric is an important task. Check the further readings section at the end of this notebook, if you’re interested!
Recall that the Euclidean distance \(d_2\) between two column vectors \(\mathbf{x}\) and \(\mathbf{y}\) is defined as the square root of the norm of the difference \(\mathbf{x} - \mathbf{y}\) of the two vectors, i.e.,
In the equation above, \(M\) denotes the dimensionality of the activation vector. Using Euclidean distance, let’s compute the dissimilarity between the activations produced by the first and second image!
# We extract the activations ...
x = activations['alexnet'][0]
y = activations['alexnet'][1]
# ... and compute their Euclidean distance!
d_xy = torch.sqrt(torch.dot(x - y, x - y))
display(round(d_xy.item(), 2))
79.44
We now know that the two activity patterns elicited by the first two images are approximately 79 units apart in AlexNet’s representational space. Next, we need to compute all the remaining pairwise dissimilarities. In total, there are \(N (N-1) / 2\) dissimilarities that we have to compute.
We could do so by using a nested for-loop to compute all of these dissimilarities, which could look something like this:
N = len(A) # number of stimuli
X = torch.empty((N, N), dtype=torch.float)
for i = 1, ..., N - 1:
for j = i + 1, ... N:
X[i][j] = torch.sqrt(torch.dot(A[i] - A[j], A[i] - A[j]))
X += torch.t(X)
Here, \(\mathbf{X}\) is the representational similarity matrix we want to compute, and \(\mathbf{A}\) represents the tensor of activations (e.g., activations['alexnet']). While this implementation does take advantage of the fact that \(\mathbf{X}\) is symmetric, it is still inefficient since the for-loop has to be executed sequentially and cannot be run in parallel.
To speed things up drastically, we can vectorize our code to take advantage of the performance boost provided by parallelization. Doing so involves a bit of linear algebra. Feel free to skip the details! All we’re doing really is to find a closed-form expression that lets us compute all pairwise distances at once, eliminating the need for a for-loop.
For the math-savvy readers out there, keep on reading. First, observe that the squared Euclidean distance between \(\mathbf{x}\) and \(\mathbf{y}\) can be rewritten as follows:
Let \(\mathbf{x}^{\top} = \mathbf{A}_{i,:}\) and \(\mathbf{y}^{\top} = \mathbf{A}_{j,:}\) correspond to two rows of an \(N \times M\) matrix \(\mathbf{A}\) of activations. Note that \(\mathbf{A}_{i,:}\) and \(\mathbf{A}_{j,:}\) are row vectors by definition. By setting these equal to \(\mathbf{x}^{\top}\) and \(\mathbf{y}^{\top}\), respectively, we stick to our convention of working with column vectors \(\mathbf{x}\) and \(\mathbf{y}\). Rewriting (1), we get
The last identity follows from the definition of matrix multiplication and the observation that the transpose of the \(j\)-th row of \(\mathbf{A}\) is equal to the \(j\)-th column of \(\mathbf{A}^{\top}\), i.e., \((\mathbf{A}_{j,:})^{\top} = (\mathbf{A}^{\top})_{:,j}\). Next comes the slightly creative part. We introduce another matrix \(\mathbf{B}\) whose entry at position \((i, j)\) is given by
Note that \(B_{i,j}\) only depends on \(i\). In other words, \(\mathbf{B}\) is simply a column vector that’s replicated and stacked next to each other \(N\) times. Consequently, \(\mathbf{B}^{\top}\) is a row vector that’s stacked underneath each other multiple times. In particular, we have
Hence, we can plug the definition of \(\mathbf{B}\) given in (3) into equation (2) to arrive at
What’s conceptually important here is that the pairwise dissimilarity between any pair of stimuli corresponds to an entry in a single matrix (the RHS of (4)) that we can compute in a single go. That is, the element-wise square root of the matrix on the RHS of (4) is our representational dissimilarity matrix! Since we will be computing RDMs for multiple networks, we implement (4) as a function.
def compute_rdm(
activations: torch.Tensor,
normalize_distances: bool = True
) -> torch.Tensor:
"""Compute an RDM using (normalized) Euclidean distance.
Args:
activations: The matrix of activations from which to compute the
RDM. Must be a 2-D tensor of size (N, M), where N is the
number of stimuli, and M 2 is the number of unit activations
per stimulus.
normalize_distances: Whether to normalize the squared pairwise
distances (i.e., before taking the square root) by the number
M of unit activations per stimulus.
Returns:
The RDM computed from the data using Euclidean distance as a 2-D
tensor.
"""
# Compute squared pairwise distances
norms_squared = torch.sum(torch.square(activations), dim=1, keepdim=True) # B as defined in (3)
distances_squared = norms_squared + norms_squared.T - 2 * torch.mm(activations, activations.T) # RHS of (4)
# Clamp values to 0 (to potentially correct for numerical inaccuracies)
distances_squared = torch.clamp(distances_squared, min=0.0)
# Normalize Euclidean distances by number of units M
rdm = distances_squared / activations.size(dim=1) if normalize_distances else distances_squared
# Compute element-wise square root
return torch.sqrt(rdm)
Next, let’s use this function to compute the RDMs for all our networks.
raw_rdms = {}
for model, activation in activations.items():
raw_rdms[model] = compute_rdm(activation, True)
Finally, before we compare these RDMs to each other, let’s visualize them! To do so, we convert the raw entries of the RDMs (i.e., the true dissimilarities) to percentiles. This is commonly done in practice since doing so makes it easier to compare multiple RDMs to each other. Additionally, it highlights any structures present in the RDMs. At the same time, one should always be aware of this very fact! That is, it may appear as if there is a very clear and distinct structure present in an RDM even when the true differences between the raw entries of the RDM are very small.
# Convert to percentiles
percentile_rdms = {}
for model in ['alexnet', 'resnet50', 'vgg11', 'vit_b16']:
raw_rdm = raw_rdms[model]
percentiles = percentileofscore(raw_rdm.flatten().cpu(), raw_rdm.flatten().cpu(), kind='rank')
percentile_rdms[model] = percentiles.reshape(raw_rdm.shape)
# Prepare plot
fig, axes = plt.subplots(1, 4, figsize=(12, 4))
# Plot RDMs
with sns.plotting_context('notebook'):
for ax, model in zip(axes, ['alexnet', 'resnet50', 'vgg11', 'vit_b16']):
sns.heatmap(
percentile_rdms[model],
vmin=0,
vmax=100,
cmap='viridis',
cbar=False,
square=True,
ax=ax
)
ax.set_title(model)
ax.set_xticks([])
ax.set_yticks([])
# Add title
fig.suptitle('Representational Dissimilarity Matrices')
# Add colorbar
pos = ax.get_position()
cbar_ax = fig.add_axes([pos.x1 + 0.01, 0.218, 0.01, 0.56])
cbar = fig.colorbar(axes[-1].collections[0], cax=cbar_ax)
cbar.set_ticks([0, 100])
cbar.set_ticklabels([0, 100])
cbar.ax.tick_params(size=0)
cbar.set_label('percentiles', rotation=90, labelpad=-15)
plt.subplots_adjust(wspace=0.05)
plt.show()
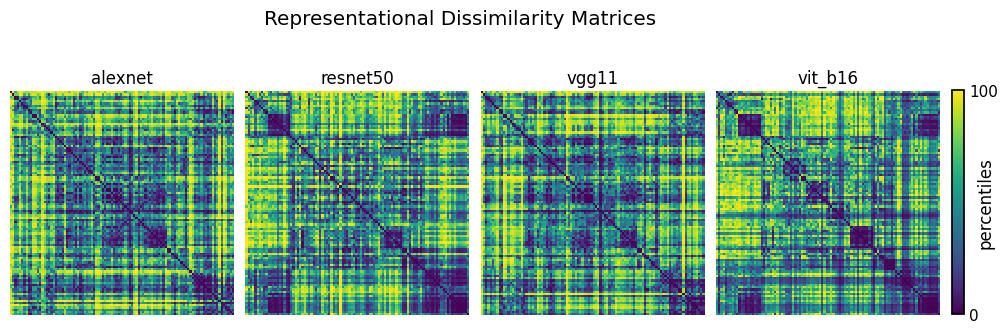
From visual inspection alone, it seems as if the representations of AlexNet and VGG11 are quite similar, and so are the representations of ResNet-50 and ViT-B/16. Let’s find out if this also holds analytically in the next section!
Step 2: Comparing Representations#
We want to find out whether the RDMs produced by two systems (here: two networks) are similar or not. Assuming that the distance function that was used to compute the RDMs is symmetric, each RDM is a symmetric matrix with \(0\)s on the diagonal. Hence, all the information characterized by a single RDM is contained in its upper triangular part, excluding the diagonal. Hence, we can extract these entries and flatten them into a single vector as illustrated in the figure below.

Once we have done so, the problem of determining whether two systems produce similar internal representations reduces to quantifying the similarity of these two vectors. Popular measures for this problem are cosine similarity and correlation measures. In this notebook, we’ll be using rank correlation to determine the similarity of two RDMs.
To get started, we need a function that lets us extract the upper triangular part of an RDM and flatten it into a vector.
def get_upper_tri_matrix(sq_matrix: torch.Tensor) -> torch.Tensor:
"""Extract the upper triangular part of a square matrix.
Args:
sq_matrix: The square matrix from which to extract the upper
triangular matrix (excluding the diagonal).
Returns:
The upper triangular matrix (excluding the diagonal) of the
square matrix ``sq_matrix``, flattened into a vector using
row-major order.
"""
mask = torch.triu(torch.ones_like(sq_matrix, dtype=torch.bool), diagonal=1)
return sq_matrix[mask]
Next, we can compute the pairwise rank correlation coefficients between all pairs of RDMs that we have computed in the previous section. There is one important detail to be pointed out here: For further analyses and visualization, we keep the quantity \(1 - \text{correlation}\) instead of the (rank) correlation itself. This simple step transforms the (rank) correlation from a similarity measure (i.e., higher values indicate higher similarity) into a dissimilarity measure (i.e., higher values indicate higher dissimilarity).
# Initialize matrix to store results
rdm_correlations = torch.zeros((4, 4))
# Compute all pairwise correlations
for row, rdm1 in enumerate(raw_rdms.values()):
for col, rdm2 in enumerate(raw_rdms.values()):
if row == col:
continue
rdm_correlations[row, col] = 1 - spearmanr( # 1 - correlation
get_upper_tri_matrix(rdm1.cpu()),
get_upper_tri_matrix(rdm2.cpu())
).statistic
display(rdm_correlations)
tensor([[0.0000, 0.7004, 0.2565, 0.7675],
[0.7004, 0.0000, 0.6104, 0.3533],
[0.2565, 0.6104, 0.0000, 0.7012],
[0.7675, 0.3533, 0.7012, 0.0000]])
The matrix rdm_correlations that we have just computed is essentially a dissimilarity matrix of dissimilarity matrices, which is sometimes referred to as a second-order dissimilarity matrix. Just staring at the raw numbers is somewhat unintuitive. Let’s visualize this matrix just like we’ve done for the previous RDMs!
# Plot data
with sns.plotting_context('notebook'):
ax = sns.heatmap(
rdm_correlations,
vmin=0,
vmax=1,
cmap='viridis',
square=True
)
# Add title, modify axes
ax.set_title('Second-Order Dissimilarity Matrix', pad=10)
ax.tick_params(left=False, bottom=False)
ax.set_xticklabels(raw_rdms.keys())
ax.set_yticklabels(raw_rdms.keys())
# Adjust colorbar
cbar = ax.collections[0].colorbar
cbar.set_label(r'$1 - \text{correlation}$', labelpad=15)
cbar.ax.tick_params(left=False, right=False)
cbar.ax.set_yticks([0, 1])
plt.show()
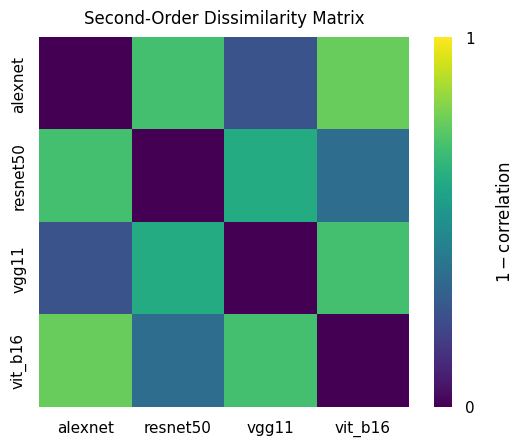
These results confirm what we had already assumed after looking at the individual RDMs: AlexNet and VGG11 are quite similar, and so are ResNet-50 and ViT-B/16, while all remaining pairs are less similar to each other. Another way of visualizing these results is to use multidimensional scaling (MDS). Multidimensional scaling is a statistical technique used to visualize the similarity or dissimilarity of (potentially high-dimensional) data in a lower-dimensional space by placing each datapoint in the low-dimensional space such that the distances between these points match the true dissimilarities as closely as possible.
For this notebook, we use the implementation of MDS provided by scikit-learn.
# Apply MDS to second-order dissimilarity matrix
mds = MDS(
n_components=2,
random_state=42,
dissimilarity='precomputed'
)
embedded_pos = mds.fit_transform(rdm_correlations)
# Preparations for plot
cmap = mpl.colormaps['viridis']
norm = Normalize(vmin=0, vmax=1)
xytexts = [
(0, 10), # AlexNet
(40, -10), # ResNet-50
(30, 5), # VGG11
(0, 10) # ViT-B/16
]
# Plot results
with sns.plotting_context('notebook'):
ax = sns.scatterplot(
x=embedded_pos[:, 0],
y=embedded_pos[:, 1],
color='black',
s=100,
zorder=2
)
# Add connecting lines
for i in range(len(embedded_pos)):
for j in range(i + 1, len(embedded_pos)):
color = cmap(norm(rdm_correlations[i, j]))
distance = np.linalg.norm(embedded_pos[i] - embedded_pos[j])
line_width = rdm_correlations[i, j] / distance
ax.plot(
[embedded_pos[i, 0], embedded_pos[j, 0]], [embedded_pos[i, 1], embedded_pos[j, 1]],
color=color,
lw=line_width,
zorder=1
)
# Add title, modify plot
ax.set_title('MDS Embedding of Second-Order Dissimilarity Matrix', pad=40)
sns.despine(left=True, bottom=True)
ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)
# Annotate individual points
labels = ['AlexNet', 'ResNet-50', 'VGG11', 'ViT-B/16']
for idx, (label, (x, y)) in enumerate(zip(labels, embedded_pos)):
ax.annotate(
label,
(x, y),
textcoords='offset points',
xytext=xytexts[idx],
ha='center'
)
plt.show()
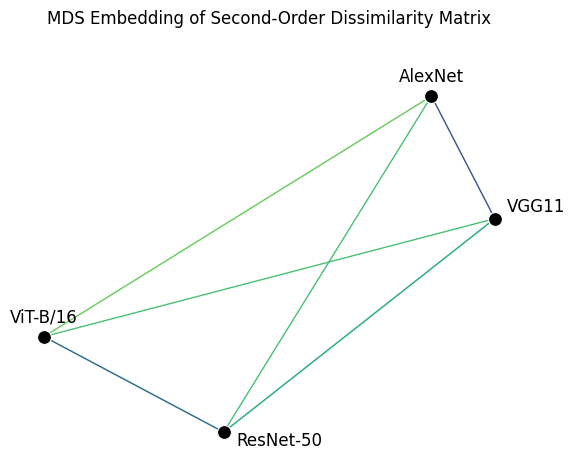
Once more, this plot confirms what we had already derived from looking at the raw dissimilarity matrices! However, it is more intuitive and quicker to interpret than the second-order dissimilarity matrix plotted above. Nevertheless, bear in mind that MDS is a dimensionality reduction technique in the sense that it attempts to represent high-dimensional data in a lower-dimensional space. When there are many points to embed in a 2-D space, the pairwise distances represented by the 2-D plot can become distorted. For that reason, it is always a good idea to include the raw data alongside an MDS plot when presenting the results of your analysis.
You have made it to the end of this notebook, congratulations! If you found this notebook helpful, please consider leaving a star 🌟 on GitHub.
Additional Material#
Exercises#
These exercises are designed to deepen your understanding of representational similarity analysis. While it’s great to work through code, there’s no better way to learn than by writing your own code. While the exercises are numbered, there is absolutely no need to follow this order when working through them. In particular, any exercise can be completed without completing any other exercise, so you can pick and choose whichever exercise sounds most interesting to you.
Try to use a different subset of images of the CIFAR10 dataset for the analysis. Do the results change? What happens if you use more/fewer images per category?
Use images from a different dataset such as CIFAR100 or ImageNet.
Include some more networks into the analysis!
Extract activations from additional layers other than the penultimate layer. Here is the documentation of the
create_feature_extractormethod that we used to extract the activations. To see the names of the layers that you can extract from, simply print the network (e.g.,print(alexnet)).Try to replace Euclidean distance by another distance measure when computing RDMs in Step 1 (e.g., correlation distance, cosine distance). Can you find a way to implement these distances without the need for a for-loop? Does the representational similarity analysis yield different results when using the new distance measure?
Similarly, try replacing the rank correlation distance in Step 2 of the analysis by a different dissimilarity measure. Again, how do the results compare to the ones obtained in this tutorial?
We used multidimensional scaling (MDS) to visually represent the second-order dissimilarity matrix of our analysis. In the same manner, we could visualize each of the (first-order) dissimilarity matrices that we obtained for the four networks included in our analysis. Try to do so! Also, what information does such a plot contain?
Literature#
Foundations & Reviews#
Representational similarity analysis - Connecting the branches of systems neuroscience (Kriegeskorte et al., 2008)
Representational geometry: Integrating cognition, computation, and the brain (Kriegeskorte and Kievit, 2013)
Peeling the onion of brain representations (Kriegeskorte and Diedrichsen, 2019)
Statistical Methods & Inference#
Reliability of dissimilarity measures for multi-voxel pattern analysis (Walther et al., 2016)
Representational structure or task structure? Bias in neural representational similarity analysis and a Bayesian method for reducing bias (Cai et al., 2019)
Comparing representational geometries using whitened unbiased-distance-matrix similarity (Diedrichsen et al., 2021)
Statistical inference on representational geometries (Schütt et al., 2023)
Applications & Challenges#
Hierarchical modular optimization of convolutional networks achieves representations similar to macaque IT and human ventral stream (Yamins et al., 2013)
Deep neural networks rival the representation of primate IT cortex for core visual object recognition (Cadieu et al., 2014)
Performance-optimized hierarchical models predict neural responses in higher visual cortex (Yamins et al., 2014)
Inferring brain-computational mechanisms with models of activity measurements (Kriegeskorte and Diedrichsen, 2016)
Representational models: A common framework for understanding encoding, pattern-component, and representational-similarity analysis (Diedrichsen and Kriegeskorte, 2017)
Individual differences among deep neural network models (Mehrer et al., 2020)
Integrative benchmarking to advance neurally mechanistic models of human intelligence (Schrimpf et al., 2020)
Obstacles to inferring mechanistic similarity using representational similarity analysis (Dujmović et al., 2023)
Conclusions about neural network to brain alignment are profoundly impacted by the similarity measure (Soni et al., 2024)
Getting aligned on representational alignment (Sucholutsky et al., 2024)
Tools, Libraries & Tutorials#
A toolbox for representational similarity analysis (Nili et al., 2014)
rsatoolbox (Python library for RSA)
Statistical inference on representational geometries (Advanced tutorial on performing statistical inference using RSA)


